1.6: Delay and Loss in Packet-Switched Networks
Having now
briefly considered the major pieces of the Internet architecture--the applications,
end systems, end-to-end transport protocols, routers, and links--let us
now consider what can happen to a packet as it travels from its source
to its destination. Recall that a packet starts in a host (the source),
passes through a series of routers, and ends its journey in another host
(the destination). As a packet travels from one node (host or router) to
the subsequent node (host or router) along this path, the packet suffers
from several different types of delays at each node along the path.
The most important of these delays are the nodal processing delay, queuing
delay, transmission delay, and propagation delay; together,
these delays accumulate to give a total nodal delay. In order to
acquire a deep understanding of packet switching and computer networks,
we must understand the nature and importance of these delays.
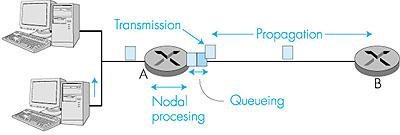
1.6.1: Types of DelayLet us explore these delays in the context of Figure 1.19. As part of its end-to-end route between source and destination, a packet is sent from the upstream node through router A to router B. Our goal is to characterize the nodal delay at router A. Note that router A has an outbound link leading to router B. This link is preceded by a queue (also known as a buffer). When the packet arrives at router A from the upstream node, router A examines the packet's header to determine the appropriate outbound link for the packet, and then directs the packet to the link. In this example, the outbound link for the packet is the one that leads to router B. A packet can be transmitted on a link only if there is no other packet currently being transmitted on the link and if there are no other packets preceding it in the queue; if the link is currently busy or if there are other packets already queued for the link, the newly arriving packet will then join the queue.
Processing Delay The time required to examine the packet's header and determine where to direct the packet is part of the processing delay. The processing delay can also include other factors, such as the time needed to check for bit-level errors in the packet that occurred in transmitting the packet's bits from the upstream router to router A. Processing delays in high-speed routers are typically on the order of microseconds or less. After this nodal processing, the router directs the packet to the queue that precedes the link to router B. (In Section 4.6 we will study the details of how a router operates.) Queuing Delay At the queue, the packet experiences a queuing delay as it waits to be transmitted onto the link. The queuing delay of a specific packet will depend on the number of other, earlier-arriving packets that are queued and waiting for transmission across the link. The delay of a given packet can vary significantly from packet to packet. If the queue is empty and no other packet is currently being transmitted, then our packet's queuing delay is zero. On the other hand, if the traffic is heavy and many other packets are also waiting to be transmitted, the queuing delay will be long. We will see shortly that the number of packets that an arriving packet might expect to find on arrival is a function of the intensity and nature of the traffic arriving to the queue. Queuing delays can be on the order of milliseconds to microseconds in practice. Transmission Delay Assuming that packets are transmitted in first-come-first-serve manner, as is common in the Internet, our packet can be transmitted once all the packets that have arrived before it have been transmitted. Denote the length of the packet by L bits, and denote the transmission rate of the link from router A to router B by R bits/sec. The rate R is determined by transmission rate of the link to router B. For example, for a 10-Mbps Ethernet link, the rate is R = 10 Mbps; for a 100-Mbps Ethernet link, the rate is R = 100 Mbps. The transmission delay (also called the store-and-forward delay, as discussed in Section 1.4) is L/R. This is the amount of time required to transmit all of the packet's bits into the link. Transmission delays are typically on the order of microseconds or less in practice. Propagation Delay Once a bit is pushed onto the link, it needs to propagate to router B. The time required to propagate from the beginning of the link to router B is the propagation delay. The bit propagates at the propagation speed of the link. The propagation speed depends on the physical medium of the link (that is, multimode fiber, twisted-pair copper wire, and so on) and is in the range of 2 • 108 meters/sec to 3 • 108 meters/sec which is equal to, or a little less than, the speed of light. The propagation delay is the distance between two routers divided by the propagation speed. That is, the propagation delay is d/s, where d is the distance between router A and router B and s is the propagation speed of the link. Once the last bit of the packet propagates to node B, it and all the preceding bits of the packet are stored in router B. The whole process then continues with router B now performing the forwarding. In wide-area networks, propagation delays are on the order of milliseconds. Comparing Transmission and Propagation Delay Newcomers to the field of computer networking sometimes have difficulty understanding the difference between transmission delay and propagation delay. The difference is subtle but important. The transmission delay is the amount of time required for the router to push out the packet; it is a function of the packet's length and the transmission rate of the link, but has nothing to do with the distance between the two routers. The propagation delay, on the other hand, is the time it takes a bit to propagate from one router to the next; it is a function of the distance between the two routers, but has nothing to do with the packet's length or the transmission rate of the link. An analogy might clarify the notions of transmission and propagation delay. Consider a highway that has a toll booth every 100 kilometers. You can think of the highway segments between toll booths as links and the toll booths as routers. Suppose that cars travel (that is, propagate) on the highway at a rate of 100 km/ hour (that is, when a car leaves a toll booth, it instantaneously accelerates to 100 km/hour and maintains that speed between toll booths). Suppose that there is a caravan of 10 cars that are traveling together, and that these 10 cars follow each other in a fixed order. You can think of each car as a bit and the caravan as a packet. Also suppose that each toll booth services (that is, transmits) a car at a rate of one car per 12 seconds, and that it is late at night so that the caravan's cars are the only cars on the highway. Finally, suppose that whenever the first car of the caravan arrives at a toll booth, it waits at the entrance until the nine other cars have arrived and lined up behind it. (Thus the entire caravan must be "stored" at the toll booth before it can begin to be "forwarded.") The time required for the toll booth to push the entire caravan onto the highway is 10/(5 cars/minute) = 2 minutes. This time is analogous to the transmission delay in a router. The time required for a car to travel from the exit of one toll booth to the next toll booth is 100 km/(100 km/hour) = 1 hour. This time is analogous to propagation delay. Therefore, the time from when the caravan is "stored" in front of a toll booth until the caravan is "stored" in front of the next toll booth is the sum of "transmission delay" and "the propagation delay"--in this example, 62 minutes. Let's explore this analogy a bit more. What would happen if the toll-booth service time for a caravan were greater than the time for a car to travel between toll booths? For example, suppose cars travel at rate 1,000 km/hr and the toll booth services cars at rate one car per minute. Then the traveling delay between toll booths is 6 minutes and the time to serve a caravan is 10 minutes. In this case, the first few cars in the caravan will arrive at the second toll booth before the last cars in caravan leave the first toll booth. This situation also arises in packet-switched networks--the first bits in a packet can arrive at a router while many of the remaining bits in the packet are still waiting to be transmitted by the preceding router. If we let dproc, dqueue, dtrans, and dprop denote the processing, queuing, transmission, and propagation delays, then the total nodal delay is given by dnodal = dproc + dqueue + dtrans + dprop The contribution of these delay components can vary significantly. For example, dprop can be negligible (for example, a couple of microseconds) for a link connecting two routers on the same university campus; however, dprop is hundreds of milliseconds for two routers interconnected by a geostationary satellite link, and can be the dominant term in dnodal. Similarly, dtrans can range from negligible to significant. Its contribution is typically negligible for transmission rates of 10 Mbps and higher (for example, for LANs); however, it can be hundreds of milliseconds for large Internet packets sent over 28.8 Kbps modem links. The processing delay, dproc, is often negligible; however, it strongly influences a router's maximum throughput, which is the maximum rate at which a router can forward packets. Queuing Delay The most complicated and interesting component of nodal delay is the queuing delay, dqueue. In fact, queuing delay is so important and interesting in computer networking that thousands of papers and numerous books have been written about it [Bertsekas 1991; Daigle 1991; Kleinrock 1975, 1976; Ross 1995]! We give only a high-level, intuitive discussion of queuing delay here; the more curious reader may want to browse through some of the books (or even eventually write a Ph.D. thesis on the subject!). Unlike the other three delays (namely, dproc, dtrans, and dprop), the queuing delay can vary from packet to packet. For example, if 10 packets arrive at an empty queue at the same time, the first packet transmitted will suffer no queuing delay, while the last packet transmitted will suffer a relatively large queuing delay (while it waits for the other nine packets to be transmitted). Therefore, when characterizing queuing delay, one typically uses statistical measures, such as average queuing delay, variance of queuing delay, and the probability that the queuing delay exceeds some specified value. When is the queuing delay large and when is it insignificant? The answer to this question depends largely on the rate at which traffic arrives to the queue, the transmission rate of the link, and the nature of the arriving traffic, that is, whether the traffic arrives periodically or whether it arrives in bursts. To gain some insight here, let a denote the average rate at which packets arrive to the queue (a is in units of packets/sec). Recall that R is the transmission rate, that is, it is the rate (in bits/sec) at which bits are pushed out of the queue. Also suppose, for simplicity, that all packets consist of L bits. Then the average rate at which bits arrive to the queue is La bits/sec. Finally, assume that the queue is very big, so that it can hold essentially an infinite number of bits. The ratio La/R, called the traffic intensity, often plays an important role in estimating the extent of the queuing delay. If La/R > 1, then the average rate at which bits arrive to the queue exceeds the rate at which the bits can be transmitted from the queue. In this unfortunate situation, the queue will tend to increase without bound and the queuing delay will approach infinity! Therefore, one of the golden rules in traffic engineering is: Design your system so that the traffic intensity is no greater than 1. Now consider
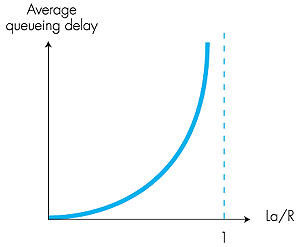
the case La/R The two examples described above of periodic arrivals are a bit academic. Typically, the arrival process to a queue is random, that is, the arrivals do not follow any pattern; packets are spaced apart by random amounts of time. In this more realistic case, the quantity La/R is not usually sufficient to fully characterize the delay statistics. Nonetheless, it is useful in gaining an intuitive understanding of the extent of the queuing delay. In particular, if traffic intensity is close to zero, then packet arrivals are few and far between and it is unlikely that an arriving packet will find another packet in the queue. Hence, the average queuing delay will be close to zero. On the other hand, when the traffic intensity is close to 1, there will be intervals of time when the arrival rate exceeds the transmission capacity (due to the burstiness of arrivals), and a queue will form. As the traffic intensity approaches 1, the average queue length gets larger and larger. The qualitative dependence of average queuing delay on the traffic intensity is shown in Figure 1.20.
One important aspect of Figure 1.20 is the fact that as the traffic intensity approaches 1, the average queuing delay increases rapidly. A small percentage increase in the intensity will result in a much larger percentage-wise increase in delay. Perhaps you have experienced this phenomenon on the highway. If you regularly drive on a road that is typically congested, the fact that the road is typically congested means that its traffic intensity is close to 1. If some event causes an even slightly larger-than-usual amount of traffic, the delays you experience can be huge. Packet Loss In our discussions above, we have assumed that the queue is capable of holding an infinite number of packets. In reality a queue preceding a link has finite capacity, although the queuing capacity greatly depends on the switch design and cost. Because the queue capacity is finite, packet delays do not really approach infinity as the traffic intensity approaches 1. Instead, a packet can arrive to find a full queue. With no place to store such a packet, a router will drop that packet; that is, the packet will be lost. From an end-system viewpoint, this will look like a packet having been transmitted into the network core, but never emerging from the network at the destination. The fraction of lost packets increases as the traffic intensity increases. Therefore, performance at a node is often measured not only in terms of delay, but also in terms of the probability of packet loss. As we shall discuss in the subsequent chapters, a lost packet may be retransmitted on an end-to-end basis, by either the application or by the transport layer protocol. End-to-End Delay Our discussion up to this point has been focused on the nodal delay, that is, the delay at a single router. Let us conclude our discussion by briefly considering the delay from source to destination. To get a handle on this concept, suppose there are Q-1 routers between the source host and the destination host. Let us also suppose that the network is uncongested (so that queuing delays are negligible), the processing delay at each router and at the source host is dproc, the transmission rate out of each router and out of the source host is R bits/sec, and the propagation delay between each pair or routers and between the source host and the first router is dprop. The nodal delays accumulate and give an end-to-end delay, dend-end = Q (dproc + dtrans + dprop) where, once again, dtrans = L/R, where L is the packet size. We leave it to the reader to generalize this formula to the case of heterogeneous delays at the nodes and to the presence of an average queuing delay at each node. |
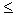 1.
Here, the nature of the arriving traffic impacts the queuing delay. For
example, if packets arrive periodically, that is, one packet arrives every
L/R seconds, then every packet will arrive to an empty queue and
there will be no queuing delay. On the other hand, if packets arrive in
bursts but periodically, there can be a significant average queuing delay.
For example, suppose N packets arrive at the same time every (L/R)N
seconds. Then the first packet transmitted has no queuing delay; the second
packet transmitted has a queuing delay of L/R seconds; and more
generally, the nth packet transmitted has a queuing delay of (n
- 1)L/R seconds. We leave it as an exercise for the reader to calculate
the average queuing delay in this example.
1.
Here, the nature of the arriving traffic impacts the queuing delay. For
example, if packets arrive periodically, that is, one packet arrives every
L/R seconds, then every packet will arrive to an empty queue and
there will be no queuing delay. On the other hand, if packets arrive in
bursts but periodically, there can be a significant average queuing delay.
For example, suppose N packets arrive at the same time every (L/R)N
seconds. Then the first packet transmitted has no queuing delay; the second
packet transmitted has a queuing delay of L/R seconds; and more
generally, the nth packet transmitted has a queuing delay of (n
- 1)L/R seconds. We leave it as an exercise for the reader to calculate
the average queuing delay in this example.