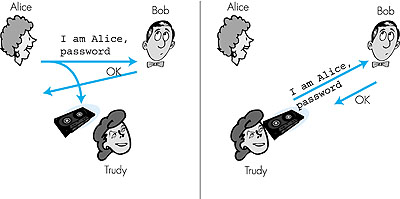
In this section we consider how one party can authenticate another party when the two are communicating over a network. We focus here on authenticating a "live" party, at the point in time when communication is actually occurring. We will see that this is a subtly different problem from proving that a message received at some point in the past (for example, that may have been archived) did indeed come from that claimed sender. This latter problem is referred to as the digital signature problem, which we explore in Section 7.4. 

When performing authentication over the network, the communicating parties cannot rely on biometric information, such as a visual appearance or a voiceprint. Indeed, we will see in our later case studies that it is often network elements such as routers and client/server processes that must authenticate each other. Here, authentication must be done solely on the basis of messages and data exchanged as part of an authentication protocol. Typically, an authentication protocol would run before the two communicating parties run some other protocol (for example, a reliable data-transfer protocol, a routing table exchange protocol, or an e-mail protocol). The authentication protocol first establishes the identities of the parties to each others' satisfaction; only after authentication do the parties get down to the work at hand. 

As in the case of our development of a reliable data-transfer (rdt) protocol, in Chapter 3, we will find it instructive here to develop various versions of an authentication protocol, which we will call ap ("authentication protocol"), and poke holes (that is, find security flaws) in each version as we proceed. Let's begin by assuming that Alice needs to authenticate herself to Bob. 

7.3.1: Authentication Protocol ap1.0

7.3.2: Authentication Protocol ap2.0

Given that we have now studied both the network and data-link layers, we know that it is not that hard (for example, if one had access to the operating system code and could build one's own operating system kernel, as is the case with Linux and several other freely available operating systems) to create an IP datagram, put whatever IP source address we want (for example, including Alice's well-known IP address) into the IP datagram, and send the datagram over the link layer protocol to the first hop router. From then on, the incorrectly source-addressed datagram would be dutifully forwarded to Bob. This approach is a form of IP spoofing, a well-known security attack technique [CERT SYN 1996]. IP spoofing can be avoided if a router is configured to refuse IP datagrams that do not have a given source IP address [RFC 2267]. For example, Trudy's first hop router could be configured to forward only datagrams containing Trudy's IP source address. However, this capability is not universally deployed or enforced. Bob would thus be foolish to assume that Trudy's network manager (who might be Trudy herself) had configured Trudy's first hop router to forward only appropriately addressed datagrams. 

7.3.3: Authentication Protocol ap3.0

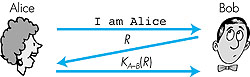
The security flaw here is clear. If Trudy eavesdrops on Alice's communication, then she can learn Alice's password. Lest you think this is unlikely, consider the fact that when one Telnets to another machine and logs in, the login password is sent unencrypted to the Telnet server. Someone connected to the Telnet client or server's LAN can possibly "sniff" (read and store) all packets transmitted on the LAN and thus steal the login password. In fact, this is a well-known approach for stealing passwords (see, for example, [Jimenez 1997]). Such a threat is obviously very real, so ap3.0 clearly won't do. 

7.3.4: Authentication Protocol ap3.1

While it is true that ap3.1 prevents Trudy from learning Alice's password, the use of cryptography here does not solve the authentication problem! Bob is again subject to a so-called playback attack: Trudy needs only eavesdrop on Alice's communication, record the encrypted version of the password, and then later play back the encrypted version of the password to Bob to pretend that she is Alice. The use of an encrypted password doesn't make the situation manifestly different from that in Figure 7.10. 

7.3.5: Authentication Protocol ap4.0

Rather than just stop here with this solution, however, let us consider a more general approach for combating the playback attack. The failure scenario in Figure 7.10 resulted from the fact that Bob could not distinguish between the original authentication of Alice and the later playback of Alice's original authentication. That is, Bob could not tell if Alice was "live" (i.e., was currently really on the other end of the connection) or whether the messages he was receiving were a recorded playback of a previous authentication of Alice. The very (very) observant reader will recall that the three-way TCP handshake protocol needed to address the same problem--the server side of a TCP connection did not want to accept a connection if the received SYN segment was an old copy (retransmission) of a SYN segment from an earlier connection. How did the TCP server side solve the problem of determining if the client was really "live"? It chose an initial sequence number that had not been used in a very long time, sent that number to the client, and then waited for the client to respond back with an ACK segment containing that number. We can adopt the same idea here for authentication purposes. 

A nonce is a number that a protocol will use only once in a lifetime. That is, once a protocol uses a nonce, it will never use that number again. Our ap4.0 protocol uses a nonce as follows: 

1. Alice sends the message, "I am Alice," to Bob. 
2. Bob chooses a nonce, R, and sends it to Alice. 
3. Alice encrypts the nonce using Alice and Bob's symmetric secret key, K_A-B, and sends the encrypted nonce, K_A-B(R) back to Bob. As in protocol ap3.1, it is the fact that Alice knows K_A-B and uses it to encrypt a value that lets Bob know that the message he receives was generated by Alice. The nonce is used to ensure that Alice is "live." 
4. Bob decrypts the received message. If the decrypted nonce equals the nonce he sent Alice, then Alice is authenticated.

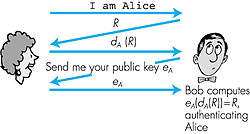
7.3.6: Authentication Protocol ap5.0

1. Alice sends the message, "I am Alice," to Bob. 
2. Bob chooses a nonce, R, and sends it to Alice. Once again, the nonce will be used to ensure that Alice is "live." 
3. Alice uses her private encryption algorithm with her private key, d_A, to the nonce and sends the resulting value d_A(R) to Bob. Since only Alice knows her private key, no one except Alice can generate d_A(R). 
4. Bob applies Alice's public encryption algorithm, e_A to the received message, that is, Bob computes e_A(d_A(R)). Recall from our discussion of RSA public key cryptography in Section 7.2 that e_A(d_A(R)) = R = d_A(e_A(R)). Thus, Bob computes R and authenticates Alice.

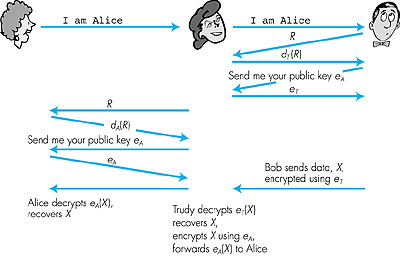
This leads to an interesting scenario, shown in Figure 7.13, in which Trudy may be able to impersonate Alice to Bob: 

1. Trudy sends the message, "I am Alice," to Bob. 
2. Bob chooses a nonce, R, and sends it to Alice, but the message is intercepted by Trudy. 
3. Trudy applies her decryption algorithm with her private key, d_T, to the nonce and sends the resulting value, d_T(R), to Bob. To Bob, d_T(R) is just a bunch of bits and he doesn't know whether the bits represent d_T(R) or d_A(R). 
4. Bob must now get Alice's public key in order to apply e_A to the value he just received. He sends a message to Alice asking her for e_A (Bob might also retrieve Alice's public key from her Web site). Trudy intercepts this message as well, and replies back to Bob with e_T, that is, Trudy's public key. Bob computes e_T(d_T(R)) = R, and thus authenticates Trudy as Alice!

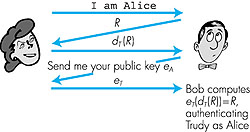
Figure 7.13: A security hold in protocol ap5.0

From the above scenario, it is clear that protocol ap5.0 is only as "secure" as is the distribution of public keys. Fortunately, there are secure ways of distributing public keys, as we will see shortly in Section 7.5. 

In the scenario in Figure 7.13, Bob and Alice might together eventually discover that something is amiss, as Bob will claim to have interacted with Alice, but Alice knows that she has never interacted with Bob. There is an even more insidious attack that would avoid this detection. In the scenario in Figure 7.14, both Alice and Bob are talking to each other, but by exploiting the same hole in the authentication protocol, Trudy is able to transparently interpose herself between Alice and Bob. In particular, if Bob begins sending encrypted data to Alice using the encryption key he receives from Trudy, Trudy can recover the plaintext of the communication from Bob to Alice. At the same time, Trudy can forward Bob's data to Alice (after re- encrypting data using Alice's real public key). 

Bob is happy to be sending encrypted data, and Alice is happy to be receiving data encrypted using her own public key; both are unaware of Trudy's presence. Should Bob and Alice meet later and discuss their interaction, Alice will have received exactly what Bob sent, so nothing will be detected as being amiss. This is one example of the so-called man-in-the-middle attack (more appropriately here, a "woman-in-the-middle" attack). It is also sometimes known as a bucket-brigade attack, since Trudy's passing of data between Alice and Bob resembles the passing of buckets of water along a chain of people (a so-called "bucket brigade") who are putting out a fire using a remote source of water.