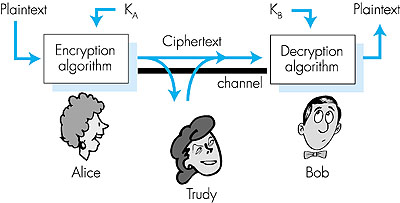
Cryptographic techniques allow a sender to disguise data so that an intruder can gain no information from the intercepted data. The receiver, of course, must be able to recover the original data from the disguised data. Figure 7.3 illustrates some of the important terminology. 

Suppose now that Alice wants to send a message to Bob. Alice's message in its original form (for example, "Bob, I love you. Alice") is known as plaintext, or cleartext. Alice encrypts her plaintext message using an encryption algorithm so that the encrypted message, known as ciphertext, looks unintelligible to any intruder. Interestingly, in many modern cryptographic systems, including those used in the Internet, the encryption technique itself is known--published, standardized, and available to everyone (for example, [RFC 1321, RFC 2437, RFC 2420]), even a potential intruder! Clearly, if everyone knows the method for encoding data, then there must be some bit of secret information that prevents an intruder from decrypting the transmitted data. This is where keys come in. 

In Figure 7.3, Alice provides a key, K_A, a string of numbers or characters, as input to the encryption algorithm. The encryption algorithm takes the key and the plaintext as input and produces ciphertext as output. Similarly, Bob will provide a key, K_B, to the decryption algorithm, that takes the ciphertext and Bob's key as input and produces the original plaintext as output. In so-called symmetric key systems, Alice and Bob's keys are identical and are secret. In public key systems, a pair of keys is used. One of the keys is known to both Bob and Alice (indeed, it is known to the whole world). The other key is known only by either Bob or Alice (but not both). In the following two subsections, we consider symmetric key and public key systems in more detail. 

Code-Breaking Contests First adopted by the U.S. government in 1977, the Data Encryption Standard (DES) 56-bit algorithm is still widely used by financial services and other industries worldwide to protect sensitive information. The company RSA has been sponsoring a series of DES-cracking contests to emphasize the need for encryption stronger than the current 56-bit standard widely used to secure both U.S. and international commerce. Each challenge is to decrypt a message that has been encoded with 56-bit DES within a specified amount of time. Code breakers meet the challenge by exhaustively searching over all of the possible secret keys. As part of the contest, RSA awards a $10,000 prize to the winners.  The company RSA launched a challenge in January 1997, aiming to show that the U.S. government's Data Encryption Standard, with its 56-bit key, offers only limited protection against a devoted adversary. The first contest was won by a team from Colorado that recovered the secret key in less than four months, winning DES Challenge I. Since that time, improved technology has made much faster exhaustive search efforts possible. In February 1998, Distributed.Net won RSA's DES Challenge II-1 with a 41-day effort, and in July, the Electronic Frontier Foundation (EFF) won RSA's DES Challenge II-2 when it cracked the DES message in 56 hours. In January 1999, Distributed.Net, a worldwide coalition of computer enthusiasts, worked with the Electronic Frontier Foundation's (EFF) "Deep Crack," a specially designed supercomputer, and a worldwide network of nearly 100,000 PCs on the Internet, to win RSA Data Security's DES Challenge III in a record-breaking 22 hours and 15 minutes. EFF's "Deep Crack" and the Distributed.Net computers were testing 245 billion keys per second when the key was found!

7.2.1: Symmetric Key Cryptography

For English text, the Caesar cipher would work by taking each letter in the plaintext message and substituting the letter that is k letters later (allowing wraparound; i.e., having the letter "z" followed by the letter "a") in the alphabet. For example if k = 3, then the letter "a" in plaintext becomes "d" in ciphertext; "b" in plaintext becomes "e" in ciphertext, and so on. Here, the value of k serves as the key. As an example, the plaintext message "bob, I love you. alice." becomes "ere, l oryh brx. dolfh." in ciphertext. While the ciphertext does indeed look like gibberish, it wouldn't take long to break the code if you knew that the Caesar cipher was being used, as there are only 25 possible key values. 

An improvement to the Caesar cipher is the so-called monoalphabetic cipher that also substitutes one letter in the alphabet with another letter in the alphabet. However, rather than substituting according to a regular pattern (for example, substitution with an offset of k for all letters), any letter can be substituted for any other letter, as long as each letter has a unique substitute letter, and vice versa. The substitution rule in Figure 7.4 shows one possible rule for encoding plaintext. 

The plaintext message "bob, I love you. alice." becomes "nkn, s gktc wky. mgsbc." Thus, as in the case of the Caesar cipher, this looks like gibberish. A monoalphabetic cipher would also appear to be better than the Caesar cipher in that there are 26! (on the order of 10²⁶) possible pairings of letters rather than 25 possible pairings. A brute force approach of trying all 10²⁶ possible pairings would require far too much work to be a feasible way of breaking the encryption algorithm and decoding the message. However, by statistical analysis of the plaintext language, for example, knowing that the letters "e" and "t" are the most frequently occurring letters in typical English text (accounting for 13% and 9% of letter occurrences), and knowing that particular two- and three-letter occurrences of letters appear quite often together (for example, "in," "it," "the," "ion," "ing," and so forth) make it relatively easy to break this code. If the intruder has some knowledge about the possible contents of the message, then it is even easier to break the code. For example, if Trudy the intruder is Bob's wife and suspects Bob of having an affair with Alice, then she might suspect that the names "bob" and "alice" appear in the text. If Trudy knew for certain that those two names appeared in the ciphertext and had a copy of the example ciphertext message above, then she could immediately determine seven of the twenty-six letter pairings, requiring 10⁹ fewer possibilities to be checked by a brute-force method. Indeed, if Trudy suspected Bob of having an affair, she might well expect to find some other choice words in the message as well. 

When considering how easy it might be for Trudy to break Bob and Alice's encryption scheme, one can distinguish three different scenarios, depending on what information the intruder has: 

• Ciphertext-only attack. In some cases, the intruder may only have access to the intercepted ciphertext, with no certain information about the contents of the plaintext message. We have seen how statistical analysis can help in a ciphertext-only attack on an encryption scheme. 
• Known-plaintext attack. We saw above that if Trudy somehow knew for sure that "bob" and "alice" appeared in the ciphertext message, then she could have determined the (plaintext, ciphertext) pairings for the letters a, l, i, c, e, b, and o. Trudy might also have been fortunate enough to have recorded all of the ciphertext transmissions and then found Bob's own decrypted version of one of the transmissions scribbled on a piece of paper. When an intruder knows some of the (plaintext, ciphertext) pairings, we refer to this as a known plaintext attack on the encryption scheme. 
• Chosen-plaintext attack. In a chosen-plaintext attack, the intruder is able to choose the plaintext message and obtain its corresponding ciphertext form. For the simple encryption algorithms we've seen so far, if Trudy could get Alice to send the message, "The quick fox jumps over the lazy brown dog," she can completely break the encryption scheme. We'll see shortly that for more sophisticated encryption techniques, a chosen-plaintext attack does not necessarily mean that the encryption technique can be broken.

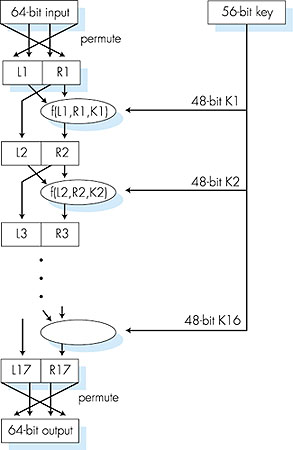
Data Encryption Standard (DES)

Let us now fast-forward to modern time and examine the Data Encryption Standard (DES) [NIST 1993], a symmetric-key encryption standard published in 1977 and updated most recently in 1993 by the U.S. National Bureau of Standards for commercial and nonclassified U.S. government use. DES encodes plaintext in 64-bit chunks using a 64-bit key. Actually, 8 of these 64 bits of the key are odd parity bits (there is one parity bit for each of the eight bytes), so the DES key is effectively 56 bits long. The National Institute of Standards (the successor to the National Bureau of Standards) states the goal of DES as follows: "The goal is to completely scramble the data and key so that every bit of the ciphertext depends on every bit of the data and every bit of the key . . . with a good algorithm, there should be no correlation between the ciphertext and either the original data or key." [NIST 1999]. 

The basic operation of DES is illustrated in Figure 7.6. In our discussion we will overview DES operation, leaving the nitty-gritty, bit-level details (there are many) to other sources [Kaufman 1995; Schneier 1995]. [Schneier 1995] includes a C implementation as well. The DES consists of two permutation steps (the first and last steps of the algorithm), in which all 64 bits are permuted and there are 16 identical "rounds" of operation in between. The operation of each round is identical, taking the output of the previous round as input. During each round, the rightmost 32 bits of the input are moved to the left 32 bits of the output. The entire 64-bit input to the ith round and the 48-bit key for the ith round (derived from the larger DES 56-bit key) are taken as input to a function that involves expansion of 4-bit input chunks into 6-bit chunks, exclusive OR-ing with the expanded 6-bit chunks of the 48-bit key Ki, a substitution operation and further exclusive OR-ing with the leftmost 32 bits of the input; see [Kaufman 1995 and Schneier 1995] for details. The resulting 32-bit output of the function is then used as the rightmost 32 bits of the round's 64-bit output, as shown in Figure 7.6. Decryption works by reversing the algorithm's operations. 

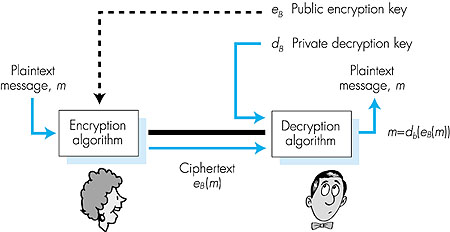
How well does DES work? How secure is it? No one can tell for sure. [Kaufman 1995]. In 1997, a network security company, RSA Data Security Inc., launched a DES Challenge contest to "crack" (decode) a short phrase it had encrypted using 56-bit DES. The unencoded phrase ("Strong cryptography makes the world a safer place.") was determined in less than four months by a team that used volunteers throughout the Internet to systematically explore the key space. The team claimed the $10,000 prize after testing only a quarter of the key space--about 18 quadrillion keys [RSA 1997]. The most recent 1999 DES Challenge III was won in a record time of a little over 22 hours, with a network of volunteers and a special purpose computer that was built for less than $250,000 (nick-named "Deep Crack") and is documented online [EFF 1999]. 

If 56-bit DES is considered too insecure, one can simply run the 56-bit algorithm multiple times, taking the 64-bit output from one iteration of DES as the input to the next DES iteration, using a different encryption key each time. For example, so-called triple-DES (3DES), is a proposed U.S. government standard [NIST 1999b] and has been proposed as the encryption standard for the Point-to-Point (PPP) protocol [RFC 2420] for the data-link layer (see Section 5.8). A detailed discussion of key lengths and the estimated time and budget needed to crack DES can be found in [Blaze 1996]. 

We should also note that our description above has considered only the encryption of a 64-bit quantity. When longer messages are encrypted, which is typically the case, DES is often used with a technique known as cipher-block chaining, in which the encrypted version of the jth 64-bit quantity of data is XOR'ed with the (j + 1)st unit of data before the (j + 1)st unit of data is encrypted. 

7.2.2: Public Key Encryption

The use of public key cryptography is quite simple. Suppose Alice wants to communicate with Bob. As shown in Figure 7.7, rather than Bob and Alice sharing a single secret key (as in the case of symmetric key systems), Bob (the recipient of Alice's messages) instead has two keys--a public key that is available to everyone in the world (including Trudy the intruder) and a private key that is known only to Bob. In order to communicate with Bob, Alice first fetches Bob's public key. Alice then encrypts her message to Bob using Bob's public key and a known (for example, standardized) encryption algorithm. Bob receives Alice's encrypted message and uses his private key and a known (for example, standardized) decryption algorithm to decrypt Alice's message. In this manner, Alice can send a secret message to Bob without either of them having to have to distribute any secret keys! 

Using the notation of Figure 7.7, for any message m, d_B(e_B(m)) = m, that is, applying Bob's public key, e_B, then Bob's private key, d_B, to the message m gives back m. We will see shortly that we can interchange the public key and private key encryption and get the same result, that is, e_B(d_B(m)) = d_B(e_B(m)) = m. 

The use of public key cryptography is thus conceptually simple. But two immediate worries may spring to mind. A first concern is that although an intruder intercepting Alice's encrypted message will only see gibberish, the intruder knows both the key (Bob's public key, which is available for all the world to see) and the algorithm that Alice used for encryption. Trudy can thus mount a chosen plaintext attack, using the known standardized encryption algorithm and Bob's publicly available encryption key to encode any message she chooses! Trudy might well try, for example, to encode messages, or parts of messages, that she suspects that Alice might send. Clearly, if public key cryptography is to work, key selection and encryption/decryption must be done in such a way that it is impossible (or at least so hard as to be nearly impossible) for an intruder to either determine Bob's private key or somehow otherwise decrypt or guess Alice's message to Bob. A second concern is that since Bob's encryption key is public, anyone can send an encrypted message to Bob, including Alice or someone claiming to be Alice. In the case of a single shared secret key, the fact that the sender knows the secret key implicitly identifies the sender to the receiver. In the case of public key cryptography, however, this is no longer the case since anyone can send an encrypted message to Bob using Bob's publicly available key. A digital signature, a topic we will study in Section 7.4 is needed to bind a sender to a message. 

While there may be many algorithms and keys that address these concerns, the RSA algorithm (named after its founders, Ron Rivest, Adi Shamir, and Leonard Adleman) has become almost synonymous with public key cryptography. Let's first see how RSA works and then examine why it works. Suppose that Bob wants to receive encrypted messages, as shown in Figure 7.7. There are two interrelated components of RSA: 

• Choice of the public key and the private key 
• The encryption and decryption algorithm

1. Choose two large prime numbers, p and q. How large should p and q be? The larger the values, the more difficult it is to break RSA, but the longer it takes to perform the encoding and decoding. RSA Laboratories recommends that the product of p and q be on the order of 768 bits for personal use and 1024 bits for corporate use [RSA Key 1999]. (Which leads one to wonder why corporate use is deemed so much more important than personal use!) 
2. Compute n = pq and z = (p - 1)(q - 1). 
3. Choose a number, e, less than n, which has no common factors (other than 1) with z. (In this case, e and z are said to be relatively prime). The letter "e" is used since this value will be used in encryption. 
4. Find a number, d, such that ed - 1 is exactly divisible (that is, with no remainder) by z. The letter "d" is used because this value will be used in decryption. Put another way, given e, we choose d such that the integer remainder when ed is divided by z is 1. (The integer remainder when an integer x is divided by the integer n, is denoted x mod n). 
5. The public key that Bob makes available to the world is the pair of numbers (n,e); his private key is the pair of numbers (n,d).

1. Suppose Alice wants to send Bob a bit pattern, or number, m, such that m < n. To encode, Alice performs the exponentiation, m^e, and then computes the integer remainder when m^e is divided by n. Thus, the encrypted value, c, of the plaintext message, m, that Alice sends is: 


c = m^e mod n

2. To decrypt the received ciphertext message, c, Bob computes 


m = c^d mod n

which requires the use of his secret key (n,d).

Table 7.1: Alice's RSA encryption, e = 5, n = 35

Plaintext letter	m: numeric representation	me	ciphertext c = me mod n
l	12	248832	17
o	15	759375	15
v	22	5153632	22
e	5	3125	10

Table 7.2: Bob's RSA decryption, d = 29, n = 35

Ciphertext c	cd	m = cd mod n	Plaintext Letter
17	481968572106750915091411825223072000	12	l
15	12783403948858939111232757568359400	15	o
22	8.5164331908653770195619449972111e+38	22	v
10	10000000000000000000000000000	5	e

Given that the "toy" example in Tables 7.1 and 7.2 has already produced some extremely large numbers, and given that we know that we saw earlier that p and q should each be several hundred bits long, several practical issues regarding RSA come to mind. How does one choose large prime numbers? How does one then choose e and d? How does one perform exponentiation with large numbers? A discussion of these important issues is beyond the scope of this book; see [Kaufman 1995] and the references therein for details. 

We do note here that the exponentiation required by RSA is a rather time- consuming process. RSA Data Security [RSA Fast 1999] says its software toolkit can encrypt/decrypt at a throughput of 21.6 Kbits per second with a 512-bit value for n and 7.4 Kbits per second with a 1024-bit value. DES is at least 100 times faster in software and between 1,000 and 10,000 times faster in hardware. As a result, RSA is often used in practice in combination with DES. For example, if Alice wants to send Bob a large amount of encrypted data at high speed, she could do the following. First Alice chooses a DES key that will be used to encode the data itself; this key is sometimes referred to as a session key, K_S. Alice must inform Bob of the session key, since this is the shared secret key they will use for DES. Alice thus encrypts the session key value using Bob's public RSA key, that is, computes c = (K_S)^e mod n. Bob receives the RSA-encrypted session key, c, and decrypts to obtain the session key, K_S. Bob now knows the session key that Alice will use for her DES-encrypted data transfer. 

Why Does RSA Work? 

The RSA encryption/decryption above appears rather magical. Why should it be that by applying the encryption algorithm and then the decryption algorithm, one recovers the original message? In order to understand why RSA works, we'll need to perform arithmetic operations using so-called modulo-n arithmetic. In modular arithmetic, one performs the usual operations of addition, multiplication, and exponentiation. However, the result of each operation is replaced by the integer remainder that is left when the result is divided by n. We will take n = pq, where p and q are the large prime numbers used in the RSA algorithm. 

Recall that under RSA encryption, a message (represented by an integer), m, is first exponentiated to the power e using modulo-n arithmetic to encrypt. Decryption is performed by raising this value to the power d, again using modulo-n arithmetic. The result of an encryption step, followed by a decryption step is thus (m^e)^d. Let's now see what we can say about this quantity. We have: 

Although we're trying to remove some of the "magic" about why RSA works, we'll need to use a rather magical result from number theory here. Specifically, we'll need the result that says if p and q are prime, and n = pq, then x^y mod n is the same as x^{(y mod (p-1)(q-1))} mod n [Kaufman 1995]. Applying this result, we have 

But remember that we chose e and d such that ed - 1 is exactly divisible (that is, with no remainder) by (p - 1)(q - 1), or equivalently that ed is divisible by (p - 1)(q - 1) with a remainder of 1, and thus ed mod (p - 1)(q - 1) = 1. This gives us 

that is, that 

This is the result we were hoping for! By first exponentiating to the power of e (that is, encrypting) and then exponentiating to the power of d (that is, decrypting), we obtain the original value, m. Even more remarkable is the fact that if we first exponentiate to the power of d and then exponentiate to the power of e, that is, we reverse the order of encryption and decryption, performing the decryption operation first and then applying the encryption operation, we also obtain the original value, m! (The proof for this result follows the exact same reasoning as above.) We will see shortly that this wonderful property of the RSA algorithm, 

will be of great use. 

The security of RSA relies on the fact that there are no known algorithms for quickly factoring a number, in this case the public value n, into the primes p and q. If one knew p and q, then given the public value e, one could then easily compute the secret key, d. On the other hand, it is not known whether or not there exist fast algorithms for factoring a number, and in this sense the security of RSA is not "guaranteed."